El número áureo aparece en muchas proporciones utilizadas en el arte y en la naturaleza.

Si se dibujara aleatoriamente un rectángulo es muy probable que el promedio de la relación entre sus dimensiones sea una proporción áurea.

La cara de una persona puede resultar armoniosa si sus elementos guardan una proporción áurea a través de rectángulos o triángulos isósceles áureos.

La naturaleza suele utilizar esa proporción a la hora de desarrollarse como ocurre con la ordenación de las semillas de un girasol, el crecimiento de las hojas en el tallo de una planta o la formación de una concha.

El número áureo proviene de establecer una relación de proporcionalidad entre dos rectángulos semejantes: un rectángulo vertical (por ejemplo) y el que resulta de eliminar el cuadrado de las dimensiones de su base. Al establecer la proporción descrita, la razón de semejanza obtenida es el número áureo. Para ello, se puede realizar el siguiente ejercicio:

En un rectángulo de base 1 unidad y de altura “a” unidades, con a > 1 aún sin determinar, se traza un segmento paralelo a su base para dividirlo en un cuadrado en la parte de abajo y un rectángulo en la de arriba. ¿Qué valor debe tener “a” para que ese rectángulo sea semejante al rectángulo inicial?

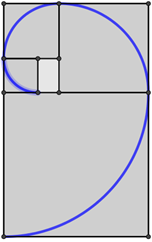
El proceso anterior se puede repetir indefinidamente con cada nuevo rectángulo que se vaya generando. A través de los cuadrados se pueden trazar cuartos de circunferencia formando una espiral. Para reproducir dicho proceso se puede utilizar GeoGebra.

Tabla

IMAGEN

ARCHIVO PDF

Presentación. ENLACE

ENLACE EXTERNO

Página web de GeoGebra:           https://www.geogebra.org/classic?lang=es

ENLACE MULTIMEDIA