Funciones 3ESO.
Como ya se vio el curso pasado, para definir un punto en el plano cartesiano se necesita un sistema de referencia formado por dos ejes numéricos, uno horizontal (eje X o eje de abscisas) y otro vertical (eje Y o eje de ordenadas). Ambos se cortan en un punto llamado origen de coordenadas a partir del cual se definen todos los demás.
Cada punto del plano está definido por su posición horizontal x y su posición vertical y, formando lo que se denomina coordenadas del punto y cuya expresión es (x, y). Los puntos se denotan usualmente con letras mayúsculas indicando la misma delante de las coordenadas: P (x, y). Al origen de coordenadas se le denota por la letra O.
Para determinar las coordenadas de un punto, se parte del origen O en horizontal para encontrar x (positiva hacia la derecha y negativa hacia la izquierda) y, posteriormente, en vertical para encontrar y (positiva hacia arriba y negativa hacia abajo). Los puntos que se sitúan sobre cualquiera de los ejes tienen como una de sus coordenadas el cero.
|
¿Cómo lo hago? |
Me cuesta hacerlo |
Estoy aprendiendo |
Lo hago bien |
Soy un experto |
|
Situar puntos en el plano si me dan las coordenadas |
|
|
|
|
|
Escribir las coordenadas de un punto si lo veo en el plano |
|
|
|
|
|
Construir una tabla a partir de un conjunto de pares de datos que aparecen en un problema |
|
|
|
|
|
Establecer ejemplos reales de funciones lineales |
|
|
|
|
|
Representar una función lineal a partir de un enunciado |
|
|
|
|
|
Representar una función lineal a partir de una tabla de valores |
|
|
|
|
|
Representar una función lineal a partir de su expresión algebraica |
|
|
|
|
|
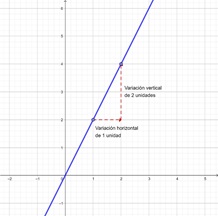
Calcular la pendiente de una recta |
|
|
|
|
|
Escribir la expresión algebraica de una función lineal a partir de su gráfica |
|
|
|
|
|
Explicar la solución de ejercicios y problemas |
|
|
|
|
|
Comprobar la solución del problema |
|
|
|
|
|
Trabajar en grupo para resolver tareas |
|
|
|
|
|
Aprender de mis errores |
|
|
|
|
|
Esforzarme para hacer bien las tareas |
|
|
|
|
IMAGEN
ARCHIVO PDF
Documento. REPASO DE GEOMETRÍA. ENLACE
ENLACE EXTERNO
Apuntes de Matemáticas
https://www.apuntesmareaverde.org.es/grupos/mat/LOMLOE/3ESOLL.htm
ENLACE MULTIMEDIA INSERTADO
FIN DEL DOCUMENTO
